Pyramidal traveling waves: a new propagating phenomenon

The Allen-Cahn equation (Nagumo equation) is a basic reaction-diffusion equation for describing two-phase problems in chemistry and in biochemistry. Researchers had been aware of one-dimensional traveling waves and of axially symmetric conical waves. Now, Taniguchi has reported the discovery of axially nonsymmetrical propagation. He describes achieving pyramidal traveling wave solutions in the Allen-Cahn equation in a mathematically rigorous manner.

A pyramidal traveling wave is among the simplest of truly three-dimensional traveling waves. It can deliver information about a cross-sectional polygon, as well as information about a one-dimensional traveling wave. Taniguchi's discovery provides basic mathematical background in support of studying three-dimensional propagations in three-dimensional chemical and biochemical media.

The contour surface of a pyramidal traveling wave solution is in the shape of a reverse pyramid. That pyramid's cross section is a polygon inscribed with a circle. Taniguchi has proved that the pyramidal traveling wave is robust under specified fluctuations. Thus has he demonstrated stable axially nonsymmetrical propagation in the Allen-Cahn equation.

M. Taniguchi
SIAM Journal on Mathematical Analysis 39, no. 1, pp. 319–344 (2007).
Department of Mathematical and Computing Sciences, Graduate School of Information Science and Engineering

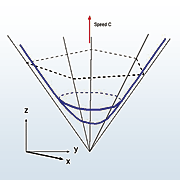
The contour surface of a pyramidal traveling wave.