A solution with a moving singularity for the Fujita equation
Published: November 30, 2011
The details of research
The Fujita equation is a type of nonlinear diffusion equation. It is known to exhibit various interesting phenomena, such as ‘blow-up’ where the maximum of a solution can tend to infinity in a finite time. Now Eiji Yanagida from the Department of Mathematics at Tokyo Institute of Technology and Shota Sato from the Mathematical Institute at Tohoku University have found a new solution that is particularly unusual for nonlinear diffusion equations.
No solutions extend to times beyond the blow-up point. On the other hand, the Fujita equation does have a stationary solution with a singularity that is radially symmetric with respect to the singularity point. Eiji Yanagida and Shota Sato have now proved the existence of a solution whose singularity moves along a prescribed curve in time. Mathematically, such a solution is called a weak solution. This is the first example of a time-dependent weak solution of a nonlinear diffusion equation.
The researchers also carefully studied the behavior of singular solutions and found one whose singularity suddenly becomes anomalous. The study of singular solutions will open up a new field of analysis on partial differential equations.
Reference
- S. Sato and E. Yanagida Solutions with moving singularities for a semilinear parabolic equation J. Differential Equations 246 (2009), 724–748 (10.1016/j.jde.2008.09.004)
- S. Sato and E. Yanagida Forward self-similar solution with a moving singularity for a semilinear parabolic equation Discrete and Continuous Dynamical Systems Series A 26 (2010), 313-331 (10.3934/dcds.2010.26.313)
- S. Sato and E. Yanagida Singular backward self-similar solutions of a semilinear parabolic equation Discrete and Continuous Dynamical Systems Series S 4 (2011), 897–906 (10.3934/dcdss.2011.4.897)
- S. Sato1 and E. Yanagida2 Appearance of anomalous singularities in a semilinear parabolic equation Communications in Pure and Applied Analysis (in press).
- Affiliations: 1 Mathematical Institute, Tohoku University, Sendai 980-8578, Japan, 2 Department of Mathematics, Tokyo Institute of Technology, Meguro-ku, Tokyo 152-8551, Japan
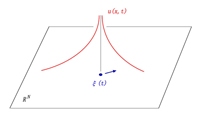
The profile of a solution u(x, t) of the Fujita equation with a moving singularity at ξ(t), where t is time, x is the spatial variable in RN.
. Any information published on this site will be valid in relation to Science Tokyo.



