Surfaces can exhibit apparent singularities, where they are not smooth. Such singularities have been investigated thoroughly in the mathematical field of topology.
In this context, the singularities of the surfaces in the left and middle figures below are equivalent. Or, more precisely, they are ‘left-right equivalent’ and are called ‘cuspidal edges’. It is well-known that cuspidal edges and ‘swallowtails’ (on the right in the figure) are generic singularities of a certain class of surfaces called ‘two-dimensional wave fronts’.
However, two of the cuspidal edges in the figure seem to be different, from a differential geometry point of view. The cuspidal edge of the left surface looks positively curved, while the middle surface looks negatively curved.
To express this observation more rigorously, Kentaro Saji at Gifu University, Masaaki Umehara at Osaka University and Kotaro Yamada at Tokyo Tech’s Department of Mathematics have introduced a new notion of ‘singular curvature’ of cuspidal edges.
“Our singular curvature provides information on the local behavior of surfaces, in particular when the surfaces have Gaussian curvature,” says Yamada. “For example, we have shown that a positively curved cuspidal edge cannot appear in surfaces with positive Gaussian curvature.”
On the other hand, when one considers the global differential geometry of wave fronts, there is a classical Gauss-Bonnet theorem for closed surfaces (without singularities) which becomes generalized for a closed wave fronts. This could be a powerful tool for researching the global properties of surfaces with singularities.
Since publishing their work in the prestigious journal Annals of Mathematics, the researchers have made several more developments in this research area.
Reference
- Authors: Kentaro Saji, Masaaki Umehara and Kotaro Yamada
- Title of original paper: The geometry of fronts
- Journal, volume, pages and year: Annals of Mathematics 169, 491--529 (2009).
- Digital Object Identifier (DOI): 10.4007/annals.2009.169.491
- Affiliations: Department of Mathematics, Graduate School of Science, Tokyo Institute of Technology.
- Department website: http://www.math.titech.ac.jp/Eng/index.html

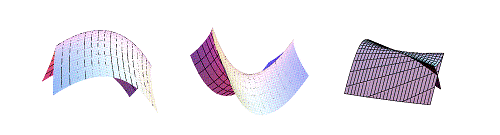
Positive cuspidal edge (left), negative cuspidal edge (middle) and the swallowtail (right)
. Any information published on this site will be valid in relation to Science Tokyo.



