The mapping class group M(S) of an orientable surface S is the group of isotopy classes of orientation-preserving homeomorphisms of S. Elements of the group are classified into three types; periodic, reducible and pseudo-Anosov.
Pseudo-Anosov mapping classes f have two numerical invariants: one is the entropy and the other is the volume of their mapping tori. Both invariants measure a type of complexity of the pseudo-Anosovs. Here, Kin and colleagues have sought to understand the connection between the two invariants.
The recent study of the Weil-Petersson geometry of Teichmüller space tells them that when they fix a surface S, the ratio of the entropy and volume for the pseudo-Anosov elements of the mapping class group on S are bounded in both directions under a bounded geometry condition. However the theory does not say very much about what might be accurate values for the bounding constants. They have now provided explicit bounding constants for the case of a punctured torus.
By using the programs by T. Hall and J. Weeks, Kin and coworkers presented various experiments for the relation between minimal entropies and volumes, and for constants bounding the entropy/volume ratio from below for pseudo-Anosov maps on disks with n punctures, Dn.
The main result is that for a punctured torus the ratio of entropy and volume is bounded by 0.1313. Restricting their attention to mapping classes of block length 1, they obtain the best possible lower bound 0.4741.
These experiments by Kin etal provide various observations and present problems on the relation between minimal entropies and minimal volumes.
Reference
- Authors: Eiko Kin, Sadayoshi Kojima, and Mitsuhiko Takasawa.
- Title of original paper: Entropy versus volume for pseudo-Anosovs.
- Journal: Experimental Mathematics 18, 397–407 (2009).
- Affiliations: Department of Mathematical and Computing Sciences, Tokyo Institute of Technology.
- Department website: http://www.is.titech.ac.jp/is-wiki/?About%20us

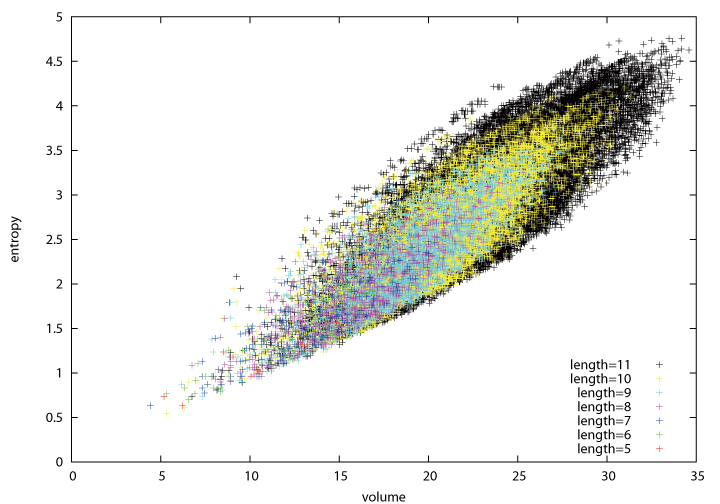
Entropy versus volume for a 6-punctured disk, D6.
. Any information published on this site will be valid in relation to Science Tokyo.



