Can gauge theory approaches describe the concept of quantum geometry?
Published: February 10, 2015
The concept of spacetime is of crucial importance in our understanding of nature. It is widely believed that even the notion of classical spacetime is of a secondary nature, and emerges from a more fundamental structure, known as quantum geometry.
However, at present it is difficult to quantize directly the concept of classical geometry. Thus, we need many approaches to obtain information about quantum geometry from other established theories such as gauge theories.
Now, Yuji Terashima at Tokyo Institute of Technology and Masahito Yamazaki at the Institute for Advanced Study have shown that 4-dimensional index for quiver gauge theories are equivalent to partition functions of 2-dimensional spin system, and a limit of the 4-dimensional index to the 3-dimensional partition function is a quantization of a geometric invariant of a 3-dimesnional manifold associated to a diagram on a torus.
These results offer a new approach to establish the concept of quantum geometry.
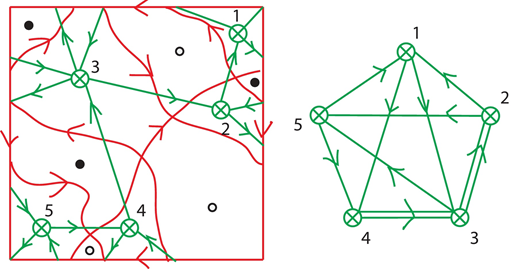
A two-dimensional torus (the square shown on the left figure) is divided by paths into regions represented by black,
white and green vertices. The right figure shows the corresponding quiver.
Reference
Authors: |
Yuji Terashima and Masahito Yamazaki |
Title of original paper: |
Emergent 3-Manifolds from Four Dimensional Superconformal Indices |
Journal, volume, pages and year: |
Phys. Rev. Lett. 109, 091602 (2012) |
Digital Object Identifier (DOI): |
|
Affiliations: |
Department of Mathematical and Computing Sciences, Tokyo Institute of Technology |
. Any information published on this site will be valid in relation to Science Tokyo.



