単体法は完全ユニモジュラーな線形計画問題に対して強多項式となりうる

概要

東京工業大学 工学院 経営工学系の水野眞治教授は、単体法^[用語1]にタルドシュ（Tardos）の基本アルゴリズムを使うことにより、完全ユニモジュラーな線形計画問題^[用語2]が強多項式^[用語3]時間で解けることを示した。この結果は、単体法で生成される解の数の上界を使うことによって達成された。また、その上界は、2012年に同系の北原知就助教との共同研究で得たものである。

単体法は図1のように実行可能領域のすべての頂点を生成することがあり、一般には多項式時間となるとは言えないが、完全ユニモジュラーな問題に限定することにより、上述の結果が得られている。この結果は、単体法により、組合せ的な線形計画問題が実際に高速に解けることに、理論的な裏付けを与える。

研究成果

線形計画問題は、内点法^[用語4]を使うことにより、多項式時間で解くことができ、さらにTardosのアルゴリズムを使うことにより、組合せ的な問題を強多項式時間で解くことができることが知られている。一方、単体法は、線形計画問題を効率よく解く方法として内点法より古くから使われているが、理論的に（強）多項式時間解法であるか、数十年にわたって不明である。今回、問題のクラスを完全ユニモジュラーな行列を持つ線形計画問題に限定した場合に、Tardosの基本アルゴリズムを使うことにより、補助問題が非退化であるという仮定のもとで、単体法が強多項式時間となることを明らかにした。

研究の背景

単体法は、ほとんどの実用上の線形計画問題を高速に解くことができるが、その根拠となる理論的な保証があまりなかった。北原・水野は、単体法で生成される解の数に関する新しい上界を得ることに最近成功した。その上界をうまく利用して、Tardosの基本アルゴリズムを使うことにより、単体法が完全ユニモジュラーな行列を持つ線形計画問題を多項式時間で解くことを示した。

今後の展開

今回の研究では、単体法が強多項式アルゴリズムとなりうることを示したが、その結果を得るために、ふたつのことを仮定している。それは、線形計画問題の制約式の係数行列が完全ユニモジュラーであることと、Tardosの基本アルゴリズムで現れる補助問題が非退化^[用語5]であることである。これらの仮定は、かなり強いものであるため、その条件を緩めたもとで、同様な結果を得ることが今後の研究の重要な課題となる。

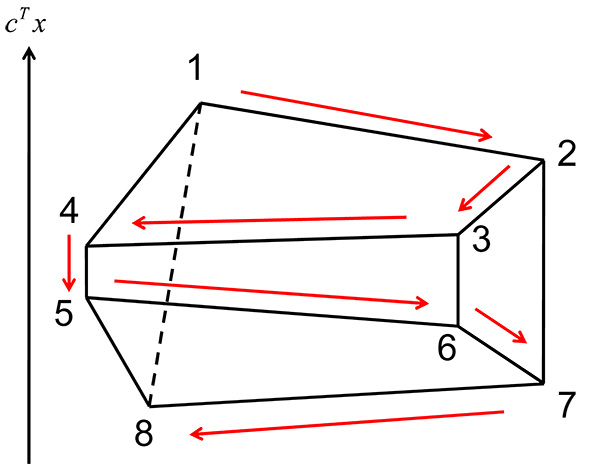
図1. 単体法で生成される点列の例

論文情報

掲載誌 :	Optimization Methods and Software Vol. 31, 1298-1304 (2016)
論文タイトル :	The simplex method using Tardos' basic algorithm is strongly polynomial for totally unimodular LP under nondegeneracy assumption
著者 :	Shinji Mizuno
所属 :	Department of Industrial Engineering and Economics, Tokyo Institute of Technology
DOI :	10.1080/10556788.2016.1208748