By unleashing the power of big data and statistical physics, researchers in Japan have developed a model that aids understanding of how and why financial Brownian motion1 arises.
Researchers at Tokyo Tech have brought the worlds of physics and finance one step closer to each other.
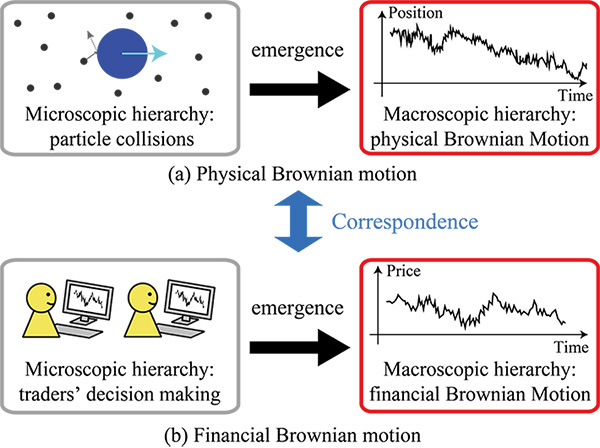
In a study published in Physical Review Letters, the team successfully demonstrated the close parallels between random movements of particles in a fluid (called physical Brownian motion) and price fluctuations in financial markets (known as financial Brownian motion).
In doing so, they revive the seminal work of French mathematician Louis Bachelier, who in 1900 was the first to describe the stochastic process2, which later became known as Brownian motion in the context of financial modeling. Extraordinarily, Bachelier's findings were published five years before Albert Einstein published his first paper on physical Brownian motion.
"The mysterious similarities between physical and financial Brownian motion have intrigued scientists for over a hundred years," the researchers say. "In our study, we have clarified how financial Brownian motion emerges from microscopic dynamics of the financial market based on direct observational data and theoretical analyses."
Looking at the US dollar–Japanese yen market, the team used big data analysis to understand what is happening at the 'microscopic' level, which boils down to the decision-making of individual foreign exchange traders.
Several studies conducted previously at Tokyo Tech by co-authors of the present study including Misako Takayasu laid the groundwork for exploring the emergence of financial Brownian motion in further detail. (For example, see Financial systems: Molecular fluid markets).
The current work, led by Kiyoshi Kanazawa and overseen by Takayasu and others, benefited from a more comprehensive dataset that became available in July 2016. This dataset enabled a meticulous approach to tracking the trend-following behavior3 of individual traders. When examined collectively, this trend-following was found to be analogous to the concept of inertia4 in physics.
In addition, the researchers were able to scale up their model to show that their approach was consistent with larger (macroscopic) dynamics. Thus, they developed a framework that parallels the kinetic theory of molecules5, which forms the theoretical basis of physical Brownian motion (see Figure 1).
They conclude that their model, rooted in standard physics, provides a solid foundation for understanding price fluctuations in stable financial markets.
They also aim to examine unstable markets vulnerable to external shocks — a hugely challenging area of research which will require better understanding of how traders react to different shocks, as well as how such behaviors could be reflected in a theoretical model.
"We strongly believe that financial markets are a good topic for hard science to tackle, thanks to recent technological breakthroughs such as big data analysis," they say.
1 Financial Brownian motion
A description of how market prices change over time based on the phenomenon of Brownian motion — the seemingly irregular motion of a particle in a liquid or gas.
2 Stochastic process
A mathematical process that appears to fluctuate randomly over time.
3 Trend-following behavior
Refers to the way in which individual traders tend to expect that future prices will move upward following an up trend, or downward in a down trend. Foreign exchange traders often try to "ride" the trend as long as possible.
4 Inertia
The law of inertia in physics states that an object remains at rest in the absence of an external force, or, if in motion, continues moving in a straight line with constant speed.
5 Kinetic theory of molecules
A model that describes the random motion of particles in a liquid or gas caused by frequent collisions with one another — this gives rise to physical Brownian motion.
Reference
Authors : |
Kiyoshi Kanazawa1,2, Takumi Sueshige2, Hideki Takayasu1,3, and Misako Takayasu1,2,* |
Title of original paper : |
Derivation of the Boltzmann Equation for Financial Brownian Motion: Direct Observation of the Collective Motion of High-Frequency Traders |
Journal : |
Physical Review Letters |
DOI : |
|
Affiliations : |
1 Institute of Innovative Research, Tokyo Institute of Technology
2 Department of Mathematical and Computing Science, Graduate School of Information Science and Engineering, Tokyo Institute of Technology
3 Sony Computer Science Laboratories
|
. Any information published on this site will be valid in relation to Science Tokyo.