東工大ニュース
東工大ニュース
公開日:2019.02.07
東京工業大学 科学技術創成研究院 先導原子力研究所の千葉敏教授らは核分裂生成物[用語1]の質量数[用語2]分布と運動エネルギーの両方における「系統性」と「特異性」を同時に説明することに世界で初めて成功した。
原子核が二つに分裂する核分裂過程では1,000種類を超える様々な核種が核分裂生成物として生成されるが、その多くが放射性原子核である。そのため適切な廃棄物処分や原子力の安全性向上のためには核分裂反応機構を解明し、核分裂生成物の質量数分布や運動エネルギーの予測を高精度に行う必要がある。
実験的には核分裂生成物の質量数分布及び運動エネルギーには有意な系統的性質と、それからずれる特異性という二つの側面があることが知られているが、これまではその両方を同時に説明できる理論は存在していなかった。
千葉教授のグループは非平衡統計力学の手法であるランジュバン方程式[用語3]を核分裂過程に適用し、核分裂生成物がほぼ同じ質量数の原子核に分裂する成分の寄与の大小と運動エネルギーの相転移的な変化の間にある相関を調べることにより核分裂における長年の謎を明らかにした。これを実現するために分裂途中の原子核の形状を表す手法と様々な形状におけるエネルギーと輸送係数[用語4]の計算手法を工夫、かつ高速の計算アルゴリズムを採用し実装した。この成果により、使用済み核燃料の適切な処理処分、廃棄物減容、有害度低減や原子炉の安全性を高めるための基礎データ構築への道が拓けた。
研究成果は英国時間2月6日10時にSpringer-Nature(シュプリンガー・ネイチャー)社の科学専門誌『Scientific Reports(サイエンティフィックリポーツ)』に掲載された。
東工大の千葉教授、Mark Dennis Usang(マーク・ デニス・ウサング)大学院生(現マレーシア原子力庁)、石塚知香子助教、Fedir Ivanyuk(フェディエール・イヴァニューク)特任教授の研究グループは、核分裂生成物の質量数分布と全運動エネルギーの系統性と特異性を同時に記述できる理論を構築した。この研究成果により、原子炉で生成する放射性原子核の量や発生する熱の予測精度が飛躍的に向上することが期待される。
研究グループはブラウン運動(熱などによる物体の不規則運動)を記述するランジュバン方程式を核分裂に適用し、核分裂の過程における原子核の形の変化を高精度に予測する理論を構築した。この方法は時間と共に変化する原子核の形を適切に表し、かつ膨大な数の形状における原子核の性質をあらかじめ予測、その情報をランジュバン方程式の入力として核分裂過程の時間発展を記述することができる。
この計算に必要となる重要な自由度を選定し、物理量を記述する適切な原子核模型を開発して精度を向上させた。この結果、核分裂により生成する原子核(核分裂生成物)の質量数分布と、生成した原子核が有する運動エネルギーがそれぞれ示す系統性(なめらかな性質)と特異性(系統性からの有意なずれ)の両方(図1)を、単一の理論で記述することに成功した。
特に、常識的にはほとんど同じ性質を有すると考えられる二つの原子核、256Fm(原子番号100番フェルミウム元素の質量数256の同位体)と258Fm(フェルミウム元素の質量数258の同位体)からの核分裂生成物の質量数分布(図2の赤丸)と運動エネルギーの顕著な違いの原因はこれまで解明されておらず、模型によってはこれらをまったく説明できなかった。
他の理論では質量数分布の違いは再現できるものの運動エネルギーについては計算すらできないというのが現状だった。同研究グループは核分裂生成物の対称成分(後述)の振る舞いを注意深く調べることにより、この相転移的な変化を原子核模型のパラメータを調整することなく、一つの模型で説明可能とした点で核分裂研究のマイルストーンといえる成果である。また、原子核の形状は最低でも4個の変数を用いて表すことが必要であることも分かった。
この研究は主として文部科学省原子力システム研究開発事業の支援を受けて、千葉教授を代表者とする事業「高速炉を活用したLLFP(長寿命の核分裂生成物)核変換システムの研究開発」で行った。
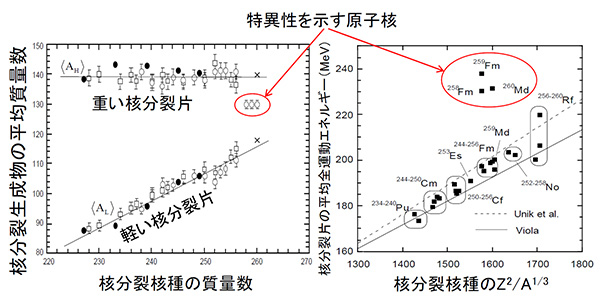
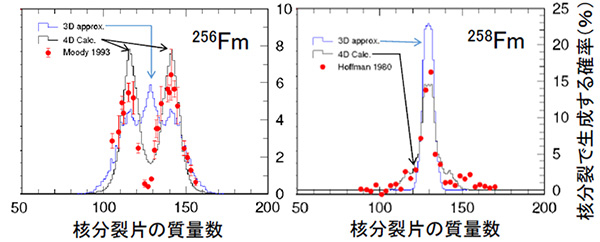
原子力で用いられるウラン領域の原子核は、核分裂によって質量数が95程度と140程度を持つ非対称な核分裂片(または核分裂生成物)を生成するため、「二山の質量数分布を持つ」と言われる。一方、ずっと重い原子核は質量数のほぼ等しい原子核に分裂し、「一山分布」である(図2、3)。その境界が質量数257であり、256Fmの核分裂片は二山分布、258Fmは一山分布である(図2)。
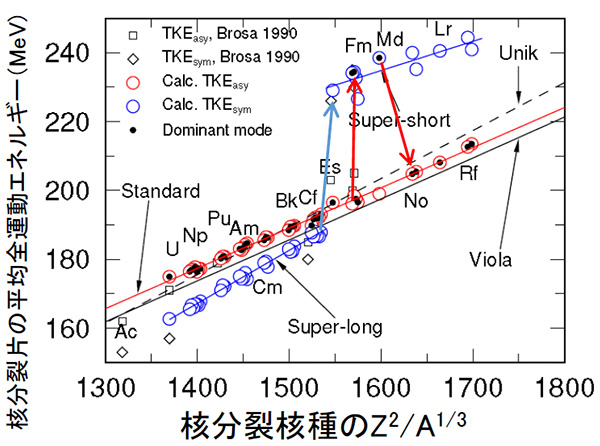
この領域で核分裂片の有する運動エネルギーの和(全運動エネルギー)も小さい値から大きい値に突然の変化を起こす(図1右)。原子炉でも核燃料を有効に使うためにはウランを長く原子炉内にとどめるため、中性子との反応により次々と質量数の大きい原子核に変わるため、このような変化が起きる可能性がある。
また宇宙における元素合成に目を向けると、中性子星[用語5]同士の合体時に起きると期待される速い中性子捕獲過程(r過程)[用語6]では「核分裂リサイクリング[用語7]」という現象が起きていると指摘されている。その場合、最終的に生成される原子核の分布は核分裂生成物の分布に強く依存するため、r過程に関与する多くの原子核の核分裂生成物分布に関する系統的な知識が必要となる。従って、どの原子核の核分裂片の分布が一山でどれが二山なのかを予測する理論が必要である。
また、核分裂では大きな熱が発生するため、r過程の起きる場所の温度を計算するために核分裂片の運動エネルギーの大きさの情報も重要である。さらに、Z=113のニホニウム元素を含む超重元素を合成する場合、核分裂は融合を阻害する主要な原因となるため、重い原子核領域における核分裂がどのようなメカニズムで起きるかを理解することが必要となるが、それに対する貴重な情報を与えるのが核分裂片の質量数分布と全運動エネルギーである。
これまで、質量数257における質量数分布と全運動エネルギーの急な変化の原因を多くの研究者が調べてきたが十分な理解が得られているわけではない。多くの理論ではこれらを全く説明できず、質量数分布についてだけは変化を説明できるが全運動エネルギーは計算すらできない、あるいは計算パラメータを調整することによってデータを説明するという状況であった。今回の研究はこの「質量数257における核分裂反応機構の転移現象」を核分裂生成物の対称成分(図3)の振る舞いを詳細に調べることで、原子核を表すパラメータの調整をせずに初めて単一の理論で説明可能とした。
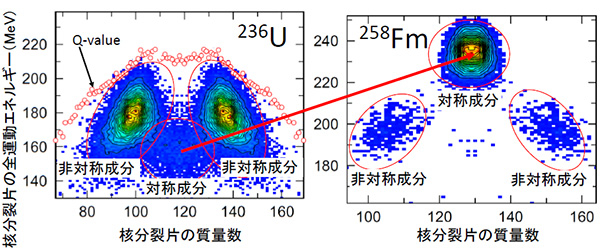
同研究グループが世界に先駆けて開発した4次元ランジュバン理論を用いてウラン領域からローレンシウム(Lr、原子番号103)領域の原子核の核分裂片の分布を計算し、生成される核分裂片対の質量数と全運動エネルギーの相関を詳細に調べた(図4)。
その結果、二つの核分裂片がほぼ等しい質量数を有する「対称成分」(図3)の形状が、質量数250から254の領域を境に、それより小さい質量数領域では長く伸びた形状、大きい質量数領域では短く接近した形状となっていることを発見した。長く伸びている場合、核分裂片の間の距離が長いためクーロン斥力が小さく運動エネルギーも小さくなるが、接近した形状ではクーロン斥力が大きくなるため運動エネルギーも大きくなる。これが「核分裂片対称成分の形状転移」である。
一方、質量数分布が二山か一山かは、主要な分裂機構が「非対称成分」であれば二山に、「対称成分」であれば一山になる。質量数の小さい領域では二山の分布を与える非対称成分(図3)が主要であるが、上記の「対称成分の形状転移」が起きるよりわずかに質量数の大きい原子核(A=257)で一山分布となる対称成分に転移する。これが「主要核分裂機構の非対称成分から対称成分への転移」である。
この主要核分裂機構はさらに質量数を上げていくと再び非対称成分へと転移する。従って主要成分の転移は2度生起することが分かった。その結果、核分裂片の質量数分布と全運動エネルギーの系統性と特異性は、この「A=250~254における対称成分の形状転移」と「主要核分裂機構のA=257における非対称成分から対称成分、さらに非対称成分への転移」という二つの転移が組み合わさって図1に示す観測量を形成するために起きていることが明らかとなった(図5)。なお、この計算において、核分裂過程における原子核の形状を最低でも4個の自由度を用いて記述することが本質的に重要であることも判明した(図2)。
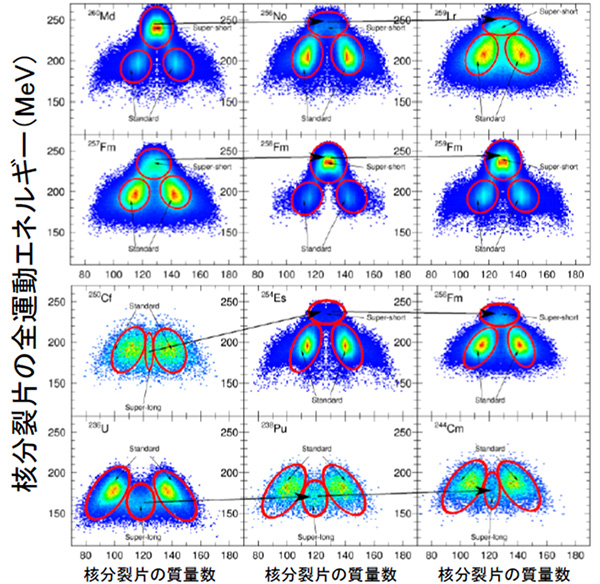
原子核は有限個の中性子や陽子からなる複雑な量子多体系であるため、原子核としての大きな変化を伴う核分裂現象は未だに多くの謎を秘めている。一方、核分裂は原子力による電力生産のみならず、宇宙での元素の起源や超重元素合成の研究にとっても重要な現象である。
同研究グループは独自に開発したランジュバン理論をさらに改良するとともに、他の理論も適用し多角的な視点から核分裂現象に肉薄し、基礎と応用の双方において学術的意義の高い成果をあげることを目指す。
用語説明
[用語1] 核分裂生成物、核分裂片 : 原子核が核分裂してできる原子核を表す。正確には、核分裂した直後にできる原子核のことを核分裂片と言い、励起した核分裂片が即発中性子(核分裂とほぼ同時に放出される中性子)を放出した後にできる原子核を核分裂生成物と言う。従って両者には質量数で1程度の差があるが、発表文においてはそれらを厳密に区別せずに用いた。
[用語2] 原子核の質量数 : 原子核はいくつかの中性子と陽子からなる。原子核中の中性子の数をN、陽子の数をZとすると、原子核の質量数AはA=N+Zで表される。原子核の陽子数は元素と1対1に対応するため、陽子数Zに相当する元素記号をXとすると、陽子数Z質量数Aの原子核はAXのように書かれる。
[用語3] ランジュバン方程式 : 揺動散逸定理に基づく運動方程式である。揺動散逸定理とは熱平衡状態において微視的な粒子の運動と巨視的に観測できる運動の間の関係を示すものであり、ブラウン運動の記述として良く知られている。これらは揺らぎと摩擦という現象として現れ、揺らぎの大きさgと摩擦の大きさγには、系の温度をTとしてアインシュタインの関係式g2=γTが成り立つ。この関係は微視的運動と巨視的運動の橋渡しの役割を担っている。核分裂モデルにおいては、微視的な運動とは原子核を構成する陽子・中性子の運動を指し、巨視的運動は原子核の形の時間的な変化を表している。核分裂の計算において熱平衡は厳密には成立しないが、系の時間発展に伴う温度変化は巨視的運動に付随してゆっくりと変化すると仮定し、瞬間瞬間においては近似的に熱平衡が成り立つとしてランジュバン方程式を適用する。
[用語4] 輸送係数 : 輸送係数は非平衡現象、あるいは熱平衡における系の時間発展を記述する理論において単位時間に単位面積を通過していく移動量と推進力をつなぐ係数のことであり、ランジュバン方程式では摩擦係数、慣性質量、拡散係数を意味する。原子核のランジュバン計算を遂行するためには原子核模型を用いてこれらを予め計算しておく必要があり、どのような自由度や模型を用いるかによって結果が異なることもある。また、これらの計算を行う際に用いる原子核模型にはパラメータが含まれるが、本研究ではすべての原子核で共通のパラメータセットを用いており、本研究で発見された転移現象は純粋にダイナミクスの効果によるものであることが結論された。
[用語5] 中性子星 : 中性子星とは中性子を主成分とする星で、半径12km程度の大きさと太陽の約1.4倍の質量を持つ高密度天体である。中性子星は太陽質量の8倍以上の重い恒星が超新星爆発を起こした際に形成されると考えられている。
[用語6] 中性子捕獲過程 : 中性子捕獲とは中性子が原子核に吸収されたのちにガンマ線を放出する核反応のことである。この中性子捕獲過程には速い中性子捕獲過程(r過程)と遅い中性子捕獲過程(s過程)がある。原子炉のような中性子束が低い環境(中性子束=105~1010個/cm2・s)下ではs過程が起きる。s過程では中性子捕獲後に次の中性子捕獲をするまでに十分時間があるため、核図表のベータ安定線に沿って安定同位体を推移しながら核子が増えていく。一方r過程は1022個/cm2・s程度の高中性子束で起きる。そのためr過程では次々に中性子が吸収され中性子ドリップライン近傍の非常に不安定な原子核が形成された後にベータ崩壊する。
[用語7] 核分裂リサイクリング : 二つの中性子星が合体する際に実現される中性子が過剰な環境でr過程が生起し、鉄領域の原子核から急激な中性子捕獲反応によってウラン、さらにはもっと重い超重元素領域までの原子核が生成すると考えられている。ウランやさらに重い原子核は中性子を吸収して核分裂したり、β崩壊をする際にも核分裂を起こしたりし、生成された重い原子核が核分裂片へと逆戻りする。一方、このようにして生成された核分裂片が中性子を吸収して再びウラン及びより重い原子核になり、核分裂により核分裂片に戻る、というサイクルが多数回起きる。これが核分裂リサイクリングである。その結果、r過程で生成する質量数が80程度より大きい原子核の存在確率は核分裂片の分布がどうであるかに強く依存する。
論文情報
掲載誌 : |
Scientific Reports |
論文タイトル : |
Correlated transitions in TKE and mass distributions of fission fragments described by 4-D Langevin equation |
著者 : |
Mark Dennis Usang, Fedir A. Ivanyuk, Chikako Ishizuka, and Satoshi Chiba |
DOI : |
お問い合わせ先
東京工業大学 科学技術創成研究院 先導原子力研究所
教授 千葉敏
E-mail : chiba.satoshi@lane.iir.titech.ac.jp
Tel : 03-5734-3066 / Fax : 03-5734-2959
取材申し込み先
東京工業大学 広報・社会連携本部 広報・地域連携部門
E-mail : media@jim.titech.ac.jp
Tel : 03-5734-2975 / Fax : 03-5734-3661