研究
研究

vol. 42
理学院 数学系 教授
利根川吉廣(Yoshihiro Tonegawa)
19世紀後半の物理学者プラトー(ベルギー、1801~1883)の名にちなんだ「プラトー問題」。これは3次元空間において曲面の面積を最小にするとはどういうことかを問う問題だ。例えば針金を自由に曲げて石鹸水に浸すと石鹸膜ができるが、この形状の数学的な性質を明らかにする。石鹸膜に関係する数学は、意外にもブラックホールの形、エンジンタービン内の燃焼面、金属加工工程の焼きなましなど幅広い分野に関係していてそれらの理解に役立つ可能性がある。
これらを扱う数学の一分野である「幾何学的測度論」を用いた「平均曲率流」の研究をけん引しているのが、理学院 数学系の利根川吉廣教授だ。
「数学者にとって問題解決の突破口となるような気付きや発見は、数年から十年に一度起こればいい方です。だからこそ、その瞬間の高揚感は何にも代えがたいものがあります」

数学者、利根川吉廣教授は数学の魅力をこう語る。そんな利根川の研究テーマは、「幾何学的測度論」と「平均曲率流」だ。聞き慣れない専門用語なので、順を追って紹介していこう。
まず、幾何学的測度論とは、どのようなものなのだろうか。ひとことで言うと、図形などの幾何学的な対象をその面積を測ることによって理解しようとする理論だ。測度論とは“量を測るための理論”という意味だ。
小中学校では、公式を用いて円や四角形などの面積を求める。さらに、高校では微積分を用いてより複雑な図形の面積を求めるようになる。しかし、これらの方法だけでは面積を求めることができないような、複雑な図形が無数に存在する。そういった図形の面積について、そもそもそれらの面積をどのように定義し計算できるのか。そのような問題意識から発展してきた分野が幾何学的測度論だ。
「現在の幾何学的測度論の研究は大きく分けて2方向あります。1つは図形の全体が部分と相似している『フラクタル』のような複雑集合について研究するもの、もう1つは3次元空間における曲面を扱う『プラトー問題』に関係する分野を研究するもので、私が研究しているのは、後者です」と利根川は語る。
プラトー問題をわかりやすく説明しよう。針金を使って自由に枠を作り、その枠を石鹸水の中に浸して持ち上げると、枠の中に石鹸膜ができる。風がなければ石鹸膜は滑らかな曲面となって静止する。この石鹸膜の形状はどのように決まっているのだろうか。石鹸膜自体には引っ張り合う力「張力」があり、なるべくその面積が小さくなるように形が決まっている、と考えるのが自然であろう。

針金で作った枠を石鹸水に浸して持ち上げると、枠の中に石鹸膜ができる。石鹸膜はとても薄いため数学的な曲面と考えられる。
プラトー問題とはこの現象を数学的に理想化した問題で、「閉じた曲線を任意に与えたとき、その曲線を境界にもち、かつ面積が最小となる曲面があることを数学的に証明せよ」という問題だ。より砕いた言葉で言えば、輪の形の針金をどんなに変形して石鹸水に入れても石鹸膜はできるのか、ということを数学的に真面目に問うているだけとも考えられる。この一見簡単そうな問題は、曲面とは何か、面積とは何かなど、一筋縄ではいかない深い数学的知見が必要となる難問なのだ。「平面上の面積は平らなものを対象としているのに対し、プラトー問題は曲面、つまり3次元内の曲がったものの面積を対象としているので、話はとても複雑になります」と利根川。面積が最小の曲面のことを、数学では「極小曲面」と呼ぶ。そのため、プラトー問題は「極小曲面の問題」ともいわれる。さらに話を進めよう。
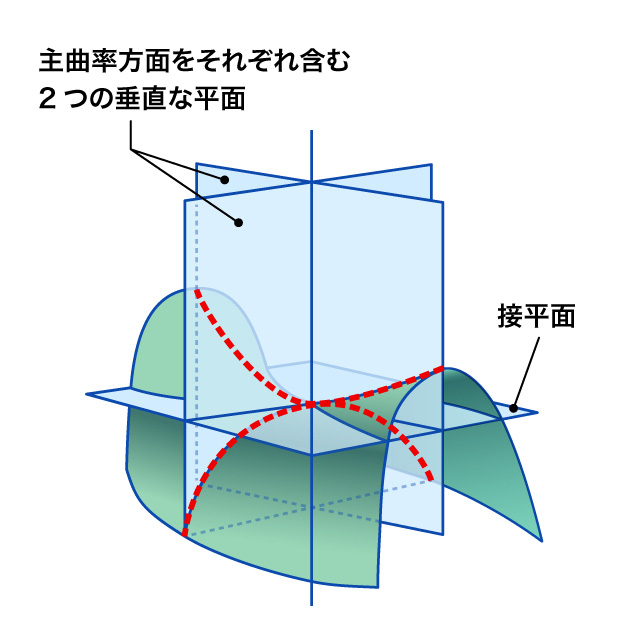 赤い2つの点線のそれぞれの曲率が2つの主曲率になる
赤い2つの点線のそれぞれの曲率が2つの主曲率になる
「石鹸膜は、物理的に実存する曲面であり、その表面は、非常に滑らかですよね。よく見ると、石鹸膜の曲がり方はどんなところでも馬にのせる鞍のように曲がっていて、その曲がり具合が各点で上下釣り合っていることがわかります。
図のように、曲面の曲がり具合を表す量として2つの『主曲率』があります。主曲率は、曲面上の各点で定義され、その2つの主曲率の平均値を『平均曲率』といいます。極小曲面は曲面上のどの点においても、平均曲率が0であることがわかっています。言い換えれば平均曲率が0になる曲面のことを、極小曲面というわけです。石鹸膜上ではこの平均曲率がちょうど0で、これは張力により面積が最小となっていることから従う性質であり、石鹸膜は極小曲面の一例です」
 赤い2つの点線のそれぞれの曲率が2つの主曲率になる
赤い2つの点線のそれぞれの曲率が2つの主曲率になる
そもそも極小曲面という概念を最初に提唱したのは、数学者ラグランジュ(フランス、1736~1813)だった。彼は数学者オイラー(スイス、1707~1783)に宛てた手紙の中で、極小曲面は「極小曲面方程式」と呼ばれる微分方程式を満たすことを示した。長い間このプラトー問題は未解決であったが、数学者ダグラス(アメリカ、1897~1965)と数学者ラドー(ハンガリー、1895~1965)は、それぞれ独立に1930年頃にこのプラトー問題を解くことに成功したのである。この業績によってダグラスは第1回目のフィールズ賞※1を受賞している。
しかし、プラトー問題を本来の石鹸膜に対して解くためには、ダグラスとラドーのアプローチでは不十分な点があった。というのも、石鹸膜は時として「特異点集合」と呼ばれる、彼らの手法では捉えるのが困難な集合を持ち得る。またダグラスとラドーの手法には次元に関する強い制限があり、一般次元で考えるプラトー問題には全く歯が立たなかったのである。

針金で作った三角錐の枠を石鹸水に浸し石鹸膜を作ると、三角錐のそれぞれの頂点から真ん中に向かって石鹸膜同士がくっついた4本の線ができる。このような点全体を「特異点集合」という。
 幾何学的測度論の基礎を築いたフェデラーによる1969年出版の著書『Geometric Measure Theory』。700ページほどの大著で、この研究分野のマイルストーンであり、その後の研究に大きな影響を与え続けている。
幾何学的測度論の基礎を築いたフェデラーによる1969年出版の著書『Geometric Measure Theory』。700ページほどの大著で、この研究分野のマイルストーンであり、その後の研究に大きな影響を与え続けている。
「このような中、1950年代にフェデラー(アメリカ、1920~2010)とフレミング(アメリカ、1928~)という2人の数学者が、プラトー問題の特異点集合の問題や次元の問題を解決できるような強力な手法を発見し、1960年に論文を発表しました。その論文は初めて幾何学的測度論を用いて極小曲面を研究した、とても影響力のある結果でした。1960年代以降、それに触発されて幾何学的測度論の研究が盛んに行われるようになり、現在に至っています。私が幾何学的測度論と出合ったのはニューヨーク大学の大学院生のときで、博士課程の指導教員だった先生の講義を聞いたのがきっかけです」
 幾何学的測度論の基礎を築いたフェデラーによる1969年出版の著書『Geometric Measure Theory』。700ページほどの大著で、この研究分野のマイルストーンであり、その後の研究に大きな影響を与え続けている。
幾何学的測度論の基礎を築いたフェデラーによる1969年出版の著書『Geometric Measure Theory』。700ページほどの大著で、この研究分野のマイルストーンであり、その後の研究に大きな影響を与え続けている。
プラトー問題を契機に始まった極小曲面の研究は、近年、より一般に界面張力が関係する様々な現象、例えば分子同士が自然に結晶や高分子を作り上げる「自己組織化」の問題や、ブラックホールにおける「事象の地平線」などの現象と深く関係することが知られている。
大学院修了後、利根川がテキサス州のライス大学で教員をしていた1995年のこと。UCバークレー校の高名な数学者エバンス(アメリカ、1949~)による集中講義を聞き、その内容に強い興味を持った。それが利根川の現在まで続く研究テーマである「平均曲率流」だ。

「平均曲率流とは、『幾何学的時間発展問題』と呼ばれるものの一種で、1970年代から研究が始まった新しい数学の一分野です。幾何学的測度論との関係は深く、簡単にいえば、曲面がある状態から極小曲面に向かうまでの過程を、数学的に考えるというものです。250年前から研究が続けられてきた極小曲面に対し、曲面を動かすという斬新な発想に、私はとてもひかれたのです。
平均曲率流は、物質科学者のマリンズ(アメリカ、1927~2001)が1958年の論文で最初に提唱しました。金属加工の過程に、『焼きなまし』というものがあります。これは金属を高温にしたのち、ゆっくりと冷やすという工程で、その過程において、結晶粒と呼ばれる金属の微粒子が無数に析出します。冷えていく過程で、結晶粒の表面では表面張力が働き、結晶粒の表面積がなるべく小さくなるように動いていくのです。その動きを記述しているのが、平均曲率流と考えられます。曲線の場合は単に曲率流と呼んだりもします」
曲率流の動画。図形がある状態から最小の長さに落ち着くまでの過程を再現している。途中で位相の変化が起こっているのがわかる。
徐々に面積が減っていく平均曲率流では途中で曲面が切れてしまったり、曲面自体がなくなってしまうなどの特異点が発生する。
 1978年にブラッケが出版した著書『The Motion of a Surface by Its Mean Curvature』。幾何学的測度論を用いた平均曲率流についての非常に革新的な内容であったが、数学の理論の確立には至っていなかった。
1978年にブラッケが出版した著書『The Motion of a Surface by Its Mean Curvature』。幾何学的測度論を用いた平均曲率流についての非常に革新的な内容であったが、数学の理論の確立には至っていなかった。
本格的な平均曲率流の研究を最初に始めたのは、プリンストン大学に所属していたブラッケ(アメリカ、1950~)だ。フェデラーと並ぶ幾何学的測度論の大家、アルムグレン(アメリカ、1933~1997)の指導の下、ブラッケは博士論文の研究結果として、平均曲率流に関する著書を1978年に出版した。この著書は平均曲率流の黎明期であるにも関わらず非常に革新的な内容だったが、一方で技術的に難解な点が多く、その内容を正確に理解できている者はいなかった。
 1978年にブラッケが出版した著書『The Motion of a Surface by Its Mean Curvature』。幾何学的測度論を用いた平均曲率流についての非常に革新的な内容であったが、数学の理論の確立には至っていなかった。
1978年にブラッケが出版した著書『The Motion of a Surface by Its Mean Curvature』。幾何学的測度論を用いた平均曲率流についての非常に革新的な内容であったが、数学の理論の確立には至っていなかった。
「1995年のエバンスの集中講義でそのことを知り、平均曲率流の理論をきちんと整備したいと思って研究し始めました。ところが、ブラッケの著書は難解で、理解はなかなか進みませんでした。その後、紆余曲折を経て平均曲率流をもう少し一般化した問題について色々研究していたのですが、2011年に『この一般化した平均曲率流に対しては、ブラッケの証明の方針のままだとうまくいかないな』と気がついたと同時に、より素直なアプローチの証明のアイデアが浮かびました。妙なもので、思いついたのは熱を出して寝込んでいて夜中に起きた時でした。それをきっかけにブラッケの著書に改めて最初から取り組みました。
ブラッケの著書は、存在定理および正則性定理が中心課題です。存在定理とは、与えられた問題に対する解を理論的に作ることができる、ということを証明することです。またこの存在定理とは別に、その作った解がどういう性質を持っているか、この場合ですと曲面なので、その動いている曲面が滑らかなのかどうなのか、という問題があります。これを正則性定理といいます。
数学ではひとつひとつの命題を最初から全て隙なく証明していくことが必要です。それは大変、忍耐と時間のかかる作業ですが、半年ほど集中して、ブラッケの主張していた平均曲率流について、まず正則性定理の証明を完成させることができました。それは2011年頃でしたが出版にしばらく時間がかかり2014年に発表しました[文献1]。その後存在定理の方に取り組み、2014年から2015年頃の期間でその証明を完成させ、これは2017年に出版されています[文献2]。前の動画で見られるような平均曲率流が数学的厳密性をもってどのように構成できるか、ということがこの存在定理によってわかりました。ブラッケの著書に出合ってから20年ほどかかりました」

これらの業績は高く評価され、この分野の専門家として利根川は世界各国からサマースクールなどの連続講義の依頼を受けるようになった。曲面が時間と共に動いていく問題は様々な工学的な問題と関係していて、例えばエンジンタービン内の燃焼面の解析などにも役立つかもしれない。そのため若手による研究の裾野の広がりに利根川は期待している。今後の研究については
「もうこれで解く問題がなくなった、ということは全くなくて、まだまだ平均曲率流について答えが分からない基礎的な問題は山積しています。一つは動いていく特異点集合の解析で、これについてはやっとスタート地点に立てたくらいです。これからも未知の問いが出てくると思います」
2015年6月にフランスのフーリエ研究所で行われた集中講義の様子。国内外で若手研究者向けの講演を積極的に行っている利根川。「まだこの分野を研究している人が少ないので、今後も若手に対する普及活動を地道に行っていきたい」と語る。2018年6月にはイタリアの国際理論物理学センターで、2019年1月にはドイツのハウスドルフ研究所で集中講義を行った。
利根川は、数学者になったきっかけをこう振り返る。「私は、子供の頃から算数や数学が好きでしたが、数学者になって生計を立てていける自信はありませんでした。しかし、大学生のとき、交換留学で行ったアメリカで命に関わるような大きな自動車事故に遭うという強烈な経験をしました。このとき、人間、いつ死ぬかわからないのだから、やりたいことをやろう!と強く思い、数学者の道を進む決心をしました」
利根川は数学の魅力について改めてこう語る。「現代社会は、科学技術の進歩が非常に速く、その分、流行り廃りも激しいですよね。一方、数学には4,000年以上にもおよぶ長い歴史があり、多くの数学者たちの努力の結晶が長い年月をかけてゆっくりゆっくり積み上げられ、今日に至っています。数学における大発見はめったに起こりませんが、その分、一度確立した理論は堅牢かつ普遍です。また、数学はただ正しければ良いというものではなく、音楽などの芸術に似たある種の美しさや重厚さという価値観があります。これらが数学の大きな魅力だと感じています」

最後に、利根川は自身の研究者人生を振り返り、学生や若い研究者にメッセージを送ってくれた。「現在はコロナ禍が続いており、渡航はむずかしい状況です。しかし、落ち着いたら、ぜひ海外留学をお勧めしたいですね。生まれ育ってきた環境の中に安住していると、知らず知らずのうちに固定観念ができてしまいます。それが揺さぶられるような経験は、若いうちでなければできないと思います。私の場合は、大学時の留学がその後の進路に決定的な影響を与えました。できれば、キャリアを決める前の段階で海外留学を経験して、視野を広げてほしいと願っています。そのためにも、専門分野はもちろん、英語の勉強にも力を入れてほしいと思いますね。英語でコミュニケーションできると活躍の場は格段に広がります」
若い数学者のすぐれた業績に対して与えられる国際的な賞。名称はこの賞を設けることを提唱したカナダの数学者ジョン・チャールズ・フィールズ(1863~1932)にちなむ。第一回目の授与は1936年。
[文献1] K. Kasai, Y. Tonegawa, A general regularity theory for weak mean curvature flow, Calc. Var. Partial Differential Equations 50, (2014) no. 1, 1-68. [10.1007/s00526-013-0626-4]
[文献2] L. Kim, Y. Tonegawa, On the mean curvature flow of grain boundaries, Annales de l'Institut Fourier (Grenoble) 67, (2017) no. 1, 43-142. [10.5802/aif.3077]

利根川吉廣(Yoshihiro Tonegawa)
理学院 数学系 教授
スペシャルトピックスでは本学の教育研究の取組や人物、ニュース、イベントなど旬な話題を定期的な読み物としてピックアップしています。SPECIAL TOPICS GALLERY から過去のすべての記事をご覧いただけます。
2022年4月掲載