Research
Research
FACES: Tokyo Tech Researchers, Issue 42
Issue 42
Yoshihiro Tonegawa
Professor, Department of Mathematics, School of Science
"Plateau's problem", named after physicist Joseph Plateau (Belgium, 1801 - 1883), relates to the minimal area of a curved surface in three-dimensional space. As an example, if you were to bend a piece of wire and then dip it in soapy water, a soap film would form, and the mathematical properties of its shape could be understood. Surprisingly, the mathematics of soap films is closely connected with a wide range of fields, including the shapes of black holes, the combustion surfaces in engine turbines, and annealing in metalworking.
Professor Yoshihiro Tonegawa of the Department of Mathematics, School of Science is a leading researcher on mean curvature flow, applying its concepts to explore the mathematics field known as geometric measure theory.
"Discoveries that become breakthroughs for mathematicians only occur once every few years or once a decade. That's why there is such a strong feeling of excitement at those moments."
Tonegawa, himself a mathematician, discussed the appeal of mathematics. His research topics are "geometric measure theory" and "mean curvature flow." These are technical terms that some readers may not be familiar with, so we begin with a basic introduction.
First of all, what is geometric measure theory? Put simply, this theory relates to understanding geometrical objects by measuring their area. Measure theory means "theories for measuring quantity."
In elementary and junior high school, we learn formulas to calculate the areas of circles, quadrilaterals, and other shapes. Then in high school, we use calculus to find the areas of more complex figures. However, there are many complicated figures whose areas cannot be calculated using these methods. So, how can the areas of such figures be determined? The field of geometric measure theory emerged from an awareness of such problems.
"Research on geometric measure theory is currently divided into two broad areas. One area studies complex sets like ‘fractals’ where the overall shape is similar to its parts, and the other area studies fields related to ‘Plateau's problem’ dealing with curved surfaces in three-dimensional space. I am studying the latter," says Tonegawa.
Let's try to understand Plateau's problem as simply as possible. Imagine that you were to take a piece of wire and bend it into an arbitrary closed shape. When you then dip that frame in soapy water and remove it, a soap film is formed inside the frame. If there is no wind, the soap film becomes a static, smooth curved surface. How was the shape of this soap film determined? Naturally, we can imagine that the soap film itself has a kind of pulling force or "tension," which means the shape is determined by creating the smallest area possible.
If you dip a wire frame into soapy water and then remove it, a soap film will be formed inside the frame. This soap film can be considered a very thin mathematically curved surface.
Plateau's problem is a mathematical idealization of this phenomenon. When you create an arbitrary closed curve, the problem is mathematically proving that there is a curved surface that has a curved boundary with the smallest possible area. More simply, it can be thought of as asking a serious mathematical question about whether a soap film can be formed regardless of the shape of the wire frame when dipped in soapy water. This seems simple. But it is actually a difficult problem that requires advanced mathematical knowledge, including knowledge related to the nature of curved surfaces and their areas. Tonegawa explains, "the area of a plane is for flat objects, while Plateau's problem is for curved surfaces, that is, the area of curved objects in three dimensions, which makes things much more complicated." A curved surface with the smallest possible area is called a "minimal surface" in mathematics. So, Plateau's problem is also called the "minimal surface problem." Now let go even deeper.
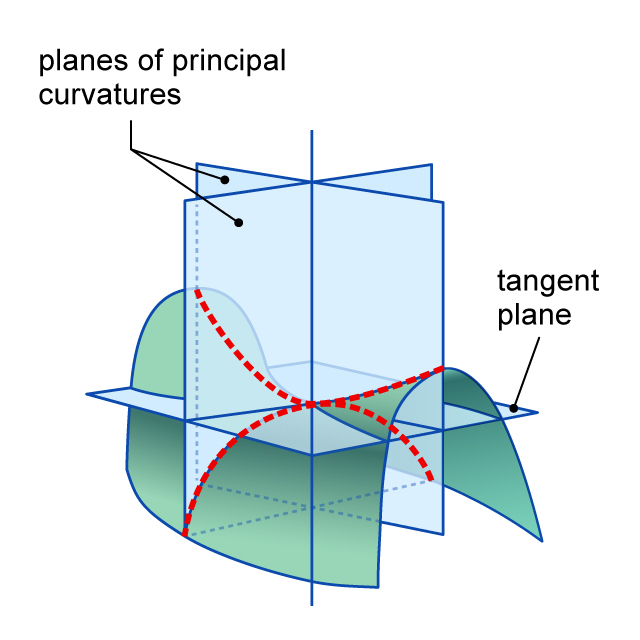The curvatures of each of the two red dotted lines are the two principal curvatures
"Soap films are curved surfaces that physically exist, and the surface is perfectly smooth! If you look closely, you will notice that the soap film curves like a horse saddle, and the degree of the curve is perfectly balanced vertically at each point.
As the figure shows, there are two ‘principal curvatures,’ which are quantities representing the degree to which a curved surface bends. A principal curvature is defined at each point along the curved surface, and the average value of the two principal curvatures is referred to as the ‘mean curvature.’ Minimal surfaces are considered to have a mean curvature of 0 at any point along the surface. Therefore, a curved surface with a mean curvature of 0 would be a minimal surface. With soap films, this mean curvature is exactly 0, and this property exists because the tension creates the smallest possible area, making the soap film an example of a minimal surface."
The curvatures of each of the two red dotted lines are the two principal curvatures
The mathematician Joseph-Louis Lagrange (France, 1736 - 1813) was the first to propose the concept of a minimal surface. In a letter to mathematician Leonhard Euler (Switzerland, 1707 - 1783), he showed that minimal surfaces satisfy a differential equation called the "minimal surface equation." Plateau's problem remained unsolved for many years until mathematicians Jesse Douglas (USA, 1897 - 1965) and Tibor Radó (Hungary, 1895 - 1965) succeeded independently in solving Plateau's problem around 1930. Douglas went on to receive the first Fields Medal1 for his efforts.
However, the approaches by Douglas and Radó were unable to solve Plateau's problem with regard to soap films. Soap films can have a set, sometimes referred to as a "singularity set," that is difficult to grasp using their methods. The approaches by Douglas and Radó also had strong dimensional restrictions, making them impractical for Plateau's problem in general dimensions.
When the frame of a triangular wire pyramid is dipped in soapy water to create a soap film, four lines are formed where the soap films meet each other, from each apex to the center. A collection of such points is referred to as a "singularity set."
Geometric Measure Theory, published in 1969 by Federer, who established the foundations for the theory. A large publication of about 700 pages, it became a milestone in the field and continues to have impact on subsequent research.
"Then, in the 1950s, mathematicians Herbert Federer (USA, 1920 - 2010) and Wendell Fleming (USA, 1928 -) established a powerful approach for solving the problems related to singularity sets and dimensions with Plateau's problem. They published a paper on this in 1960. It was the first influential result from studying minimal surfaces using geometric measure theory. This spurred research on geometrical measure theory starting from the 1960's, and it continues to be active today. I first encountered geometric measure theory in one of my doctoral classes when I was a graduate student at New York University."
Geometric Measure Theory, published in 1969 by Federer, who established the foundations for the theory. A large publication of about 700 pages, it became a milestone in the field and continues to have impact on subsequent research.
It has become well known in recent years that research on minimal surfaces, which began with Plateau's problem, is deeply connected to various phenomena related to interfacial tension, including self-organization problems where molecules naturally form crystals and polymers, and the event horizons of black holes.
After graduate school, Tonegawa became a faculty member at Rice University in Texas. In 1995, he attended an intensive course by renowned mathematician Lawrence C. Evans (USA, 1949 -) at UC Berkeley and was fascinated by its contents. It was about "mean curvature flow," and Tonegawa is still conducting research on this topic today.
"Mean curvature flow is a kind of ‘geometric time evolution problem,’ which is a new field of mathematics that started in the 1970s. It is deeply connected with geometric measure theory, and basically, it involves thinking mathematically about the process from a curved surface state to a minimal surface state. I became so interested in the novel approach of moving a curved surface in relation to a minimal surface, to solve a problem which people have been studying for 250 years."
"Mean curvature flow was first proposed by material scientist William Mullins (USA, 1927 - 2001) in a 1958 paper. In metal processing, there is a process called annealing. In the process of slowly cooling heated metal, countless fine metal particles called crystal grains are deposited. During the cooling process, surface tension acts on the surface of the crystal grains causing the surface area of the crystal grains to become as small as possible. It is believed that this movement is described by mean curvature flow. For a curve, this is also simply called the curvature flow."
Video on curvature flow. It shows the process of shapes going from a certain state to the minimum state. Phase changes that occur along the way can be seen.
A singularity occurs with the mean curvature flow where the area gradually decreases, such as the curved surface being cut off in the middle, or the curved surface itself disappearing.
The Motion of a Surface by Its Mean Curvature, published by Brakke in 1978. Although it contained innovative ideas about mean curvature flow using geometric measure theory, it did not lead to the establishment of a mathematical theory.
Kenneth Brakke (USA, 1950 -) of Princeton University was the first researcher to focus on mean curvature flow. Under the guidance of Fred Almgren (USA, 1933 - 1997), an authority on geometric measure theory like Federer, Brakke published a book on mean curvature flow in 1978 based on his dissertation work. Although it was still the early days of research on mean curvature flow, his book was innovative. However, there were many unclear technical points, and no one completely understood its contents.
The Motion of a Surface by Its Mean Curvature, published by Brakke in 1978. Although it contained innovative ideas about mean curvature flow using geometric measure theory, it did not lead to the establishment of a mathematical theory.
"I learned about this in an intensive course by Evans in 1995, and I began doing research with the goal of developing a proper theory for mean curvature flow. However, Brakke's book was perplexing and difficult to understand. After a few wrong turns, I started doing research on more generalized problems related to mean curvature flow. But in 2011, I concluded that such generalized mean curvature flow will not work if you follow Brakke's proof. As soon as I realized this, I had an idea about how I could prove a more straightforward approach. It was strange, and it came to me in the middle of the night while I battled a fever. I decided to start Brakke's book all over again.
Brakke's book focuses on an existence theorem and a regularity theorem. Existence theorems involve proving that a solution to a given problem is theoretically possible. In addition to such existence theorems, it is necessary to consider what kind of property the created solution should have, and since it is a curved surface in this case, whether the moving curved surface is smooth or not. This is known as a regularity theorem.
In mathematics, you have to prove each and every proposition from the beginning, and there can be no gaps. It required much patience and time. But after about six months of intense focus, I was able to complete the proof for the regularity theorem related to Brakke's claimed mean curvature flow. That was around 2011. It still took a while before it was published in 2014[Ref. 1]. Next, I started work on the existence theorem and completed the proof between 2014 and 2015, and it was published in 2017 [Ref. 2]. The existence theorem shows how the mean curvature flow, which was shown in the previous video, can be constructed with mathematical rigor. That was about 20 years after my first encounter with Brakke's book."
These achievements were highly regarded, and being an expert in the field, Tonegawa began receiving requests to give lectures from all over the world. The problem of how curved surfaces move over time is related to many different engineering problems and could, for example, help with analyzing combustion surfaces in engine turbines. Tonegawa looks forward to further advances by the next generations of researchers. Regarding future research, he stated,
"There will always be problems that need to be solved, and there are still many basic problems related to mean curvature flow. One is analysis of moving singularity sets. We have only just reached the starting line. More and more questions will surely pop up in the future."
Intensive course given by Tonegawa at the Fourier Institute in France in June 2015. "The number of people studying mean curvature flow is still few, so I want attract more young researchers to the field." He also held intensive courses at the International Centre for Theoretical Physics in Italy in June 2018 and at the Hausdorff Research Institute for Mathematics in Germany in January 2019.
Looking back on how he became a mathematician, Tonegawa added the following. "I've been in love with math and mathematics since I was a kid, but I wasn't sure that I could make a living as a mathematician. When I was a college exchange student in the United States, I was in a serious car accident. That was a lifechanging experience. At that time, I decided to live the life I want because we don't know when we will die. I chose to follow the path of a mathematician."
Tonegawa reiterated the appeal of mathematics saying, "In modern society, science and technology are advancing extremely rapidly, and trends change quickly. On the other hand, mathematics has a 4,000-year history, and the achievements of many mathematicians have been gradually accumulating up until today. Major discoveries are rare in mathematics, but that means that once a theory is established, it is solid and universal. Also, in mathematics, it is not enough just to be correct, there is a beauty and profoundness similar to that of art and music. I feel that these are the main attractions of mathematics."
Looking back on his life in research, Tonegawa shared the following message for students and early-career researchers. "Right now, COVID-19 is still making it difficult to travel. However, after things calm down, I strongly recommend studying abroad. Our thinking easily becomes stiff when we continue living in a comfortable and familiar environment. You can only have life-changing experiences while you are young. In my case, studying abroad at university had a decisive impact on my future. I want you to experience studying abroad before deciding on your career to widen your perspective. I recommend that you focus on studying English in addition to your specialized field. If you can communicate in English, your world will expand dramatically."
An international award presented to young mathematicians for outstanding achievements. It is named after the Canadian mathematician John Charles Fields (1863 - 1932), who advocated the establishment of this award. It was first awarded in 1936.
[Ref. 1] K. Kasai, Y. Tonegawa, A general regularity theory for weak mean curvature flow, Calc. Var. Partial Differential Equations 50, (2014) no. 1, 1-68. [10.1007/s00526-013-0626-4]
[Ref. 2] L. Kim, Y. Tonegawa, On the mean curvature flow of grain boundaries, Annales de l'Institut Fourier (Grenoble) 67, (2017) no. 1, 43-142. [10.5802/aif.3077]
Yoshihiro Tonegawa
Professor, Department of Mathematics, School of Science
School of Science —Exploring the Truth and Creating Knowledge—
Information on School of Science inaugurated in April 2016
The Special Topics component of the Tokyo Tech Website shines a spotlight on recent developments in research and education, achievements of its community members, and special events and news from the Institute.
Past features can be viewed in the Special Topics Gallery.
Published: April 2022
© Tokyo Institute of Technology. All rights reserved.
